Linked lists and structural recursion
- Syntax and built-in functions for lists
- Defining the list type
- Structural induction, structural recursion, and functions on lists
- A note on lists and tail recursion
- Immutability and structural sharing
- Exercises
→ Syntax and built-in functions for lists
Linked lists are among the most commonly used data structures. The type of lists in OCaml is 'a list.
Presence of a type variable 'a tells us that it's polymorphic: you can create lists of elements of
any type, but all elements must be the of the same type. Heterogenous lists cannot be created directly,
which is good for type safety.
We will learn about syntactic sugar for lists and standard functions first, and then learn how that type is actually defined.
This is how to create a non-empty list: let xs = [1; 2; 3; 4]. The empty list is written [].
Semicolon as a list element separator may look odd, but it has advantages,
since it makes it very easy to make a list of tuples: let ys = ["foo", 1; "bar", 2].
If the separator for list and tuple elements was the same, it would require a lot
more parentheses.
The standard library defines a number of list functions in the List module.
The simplest is the List.length : 'a list -> int function that calculates list length:
let l = List.length ["foo"; "bar"; "baz"] (* l = 3 *)
Another simple function is List.rev : 'a list -> 'a list that reverses a list.
Many of the List module functions are higher order functions that use other functions as conditions
for searching, filtering, or transformation.
For example, there is a List.exists : 'a list -> ('a -> bool) -> bool function that checks if
an element matching some condition exists in a list:
let x = List.exists (fun x -> x = 0) [0; 1; 2] (* x = true *)
Using partial application of the (=) function we could make it shorter:
let x = List.exists ((=) 0) [0; 1; 2]
Many functions from that module also raise exceptions. Some third party libraries add functions
that return value of the option type instead, but in the standard library it's not the case.
Both approaches have their advantages and disadvantages. An exception-raising function can return
values of the same type as elements of the list, but forces you to handle exceptions.
A function of 'a list -> ('a -> bool) -> 'a option type would be exception-safe, but it would force
you to unwrap the option type value and handle the case of None.
If you want to stick with the
standard library, you'll need to handle exceptions.
For example, the List.find : 'a list -> ('a -> bool) -> 'a function raises Not_found exception
if it fails to find a matching element. This is how we could convert it to a function that returns
an option type instead and then use its result in pattern matching:
let find_opt xs f =
try Some (List.find xs f)
with Not_found -> None
let () =
let x = find_opt ((=) 0) [1; 2; 3] in
match x with
None -> print_endline "This list does not include zero"
| Some _ -> print_endline "This list includes zero"
The map : ('a -> 'b) -> 'a list -> 'b list) function that you are likely already familiar with from
other languages is also there. It takes a function and a list and applies the function to every element
of the list:
let squares = List.map (fun x -> x * x) [1; 2; 3]
The List.filter : ('a -> bool) -> 'a list -> 'a list function should also look familiar since it's implemented by many languages:
let evens = List.filter (fun x -> x mod 2 = 0) [1; 2; 3; 4] (* evens = [2; 4] *)
Another commonly used function is List.fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a. In some other languages
it's known as reduce. It takes a function, a list, and an initial value, and applies the function to every list
element and the accumulator. This is how we can write a function that calculates the average value of all elements
in a list:
let average xs =
let sum = List.fold_left (fun x y -> x +. y) 0.0 xs in
sum /. (float (List.length xs))
let x = average [1.0; 2.0; 3.0]
Note that fold_left is not limited to function whose both arguments are same type. The function it takes must have type
'a -> 'b -> 'a, which is more general than 'a -> 'a -> 'a. It also means the first argument of that function will be
the accumulator, while the second will be list element, since the accumulator value has type 'a, while the list is 'b list.
For functions like addition or multiplication it is not important, but for cases when it is important, the standard library
includes List.fold_right : ('a -> 'b -> 'b) -> 'a list -> 'b -> 'b function that has order of argument types reversed.
Lists in OCaml are true linked lists, which means access to their elements is strictly sequential. To retrieve an element at
a known position, you may use List.nth : 'a list -> int -> 'a function, but remember that it's O(n).
Note that it will raise a Failure exception
if list is too short. Elements are numbered from zero. This is an example of a program that will fail:
let () = Printf.printf "%d\n" @@ List.nth [1; 2; 3] 3
We could make it safer by handling the exception:
let () =
try List.nth [1; 2; 3] 3 |> Printf.printf "%d\n"
with Failure _ -> print_endline "List is too short"
Finally, if you are not planning to do anything with results of applying a function to list elements,
you can use the List.iter : ('a -> unit) -> 'a list -> unit function. This is how you can print
all elements of a list with it for example:
let () =
List.iter print_endline ["foo"; "bar"; "baz"]
→ Defining the list type
Many data structures, including linked lists, can be defined inductively.
An inductive definition consists of two parts: a base case that defines the least possible element, and an inductive step that defines how to make larger structures from it.
In terms of sum types, it can be said that an inductive type definition includes a nullary data constructor for the empty data structure and data constructors for non-empty data structures.
The list type is defined as follows:
-
An empty list (
[]) is a list (the base case). -
A pair of a value
xand a listxs(x :: xs) is also a list (the inductive step). - Nothing else is a list.
In OCaml we cannot create our own infix data constructors, but in imaginary syntax it could be written like this:
type 'a list = [] | 'a :: 'a list
So the 'a list type is simply a sum type with two data constructors, one for the empty list, and another for non-empty lists
made from a value (head) and another list (tail). The square brackets syntax is simply a syntactic sugar, and we could create
any list using the empty list value [] and the :: constructor alone. The following definitions are equivalent:
let xs = []
let ys = [1]
let ys' = 1 :: []
let ys'' = 1 :: xs
let zs = [2; 1]
let zs' = 2 :: (1 :: [])
let ws = [3; 2; 1]
let ws' = 3 :: zs
The true syntax that is using data constructors is important because it can be used in pattern matching to define any possible list pattern. Here are some list patterns:
-
[]— an empty list -
_ :: _— any non-empty list -
_ :: []— a list with exactly one element -
_ :: _ :: _— a list with at least two elements
The square brackets syntax has limited use in pattern matching. It can be used for matching on lists of known length, but it cannot express any non-empty list for example.
-
— a list of one element
- [_; _] — a list of two elements
If you want to destructure lists into its parts, you can always substitute the wildcard in those patterns with a variable name.
If special syntax for the :: infix constructor and empty list value [] didn't exist in OCaml, we could make an equivalent
definition:
type 'a list = Nil | Cons of 'a * 'a list
The names nil for the empty list and cons for a pair of a value and another list come from the Lisp programming
language that was the first language to use this approach. When reading source code aloud, it's common to refer
to the [] value as nil and the :: constructor as cons.
→ Structural induction, structural recursion, and functions on lists
Structural induction and its twin, structural recursion, is a very common technique in functional programming. They can be used for both algorithm design and algorithm correctness proving.
For functions, we can rephrase the inductive definition as follows:
- A base case that defines how to calculate function value for the least possible element (empty data structure).
- An inductive step that defines how to calculate function value for the next element if we already know it for the previous element.
This is a generalization of mathematical induction on natural numbers. We have already seen an inductive definition when we discussed the factorial function:
- Base case: 0! = 1
- Inductive step: (n + 1)! = n! * (n + 1)
The generalization of mathematical induction for data structures is known as structural induction.
Every inductive definition of a function can be naturally converted to a recursive algorithm, assuming we know how to destructure a value into its parts. For the factorial function, we had to substitute destructuring a natural number n into m + 1 with subtracting one from it.
Data structures defined as sum types can be directly destructured using pattern matching, which makes them easy to use with recursive functions.
Recursion derived from inductive definitions is known as structural recursion. A structurally recursive function only applies itself to smaller parts of the original data. Since every inductive definition includes a base case for the empty data structure, structural recursion is guaranteed to terminate.
The other kind—generative recursion that may generate new (possibly larger) data from the original arguments and apply itself to it, does not have this property and can be much harder to reason about.
Now we are ready to write our first function that works with lists. Let's write a function that calculates
list length. There are only two possible cases. The base case is the empty list, its length is zero.
Now to the inductive step: if we know that list xs has length n, then we know that list x :: xs has
length n + 1.
Or, formally:
- length [] = 0 (base case)
- length (x :: xs) = 1 + (length xs) (inductive step)
This inductive definition can be easily converted to pattern matching:
let rec length xs =
match xs with
[] -> 0
| _ :: xs' -> 1 + (length xs')
It's very easy to see that our length function is structurally recursive: every time the recursive step is handled,
length is applied to the tail of the original list, which is guaranteed to be smaller than the original list.
It's also easy to see that this implementation is not tail recursive, since the outermost 1 + (length xs') expression cannot be evaluated
until all inner expressions are evaluated. To make it tail recursive, we could use a variant of structural recursion sometimes called
structural recursion with accumulator:
let length xs =
let rec aux ys acc =
match ys with
[] -> acc
| _ :: ys' -> aux ys' (acc + 1)
in aux xs 0
As it is with tail recursive functions, it's harder to reason about it, and harder to see if it's structurally recursive or not.
It generates new data as it goes. But notice that while new data is generated in the acc variable, it is never used in pattern
matching, so the decision what to do next only depends on the value of the ys argument, and ys is only destructured and
never modified in a way that would add anything that wasn't present in the original xs list. The function that remains
structurally recursive.
The map function can also be easily reimplemented with pattern matching. There are also just two cases.
The base case is the empty list, and since it has no elements there is nothing to apply a function to, so we return it unchanged.
The inductive step is also simple: to calculate map (x :: xs) we apply f to the head and cons it with map xs.
let rec map f xs =
match xs with
[] -> []
| y :: ys -> (f y) :: (map f ys)
Some functions may require definitions with more than two cases. For example, if we want to write a function for checking is a list is sorted, we need special handling for lists with only one element in addition to the empty list.
If we limit the discussion to lists sorted in ascending order, our definition will look like this:
- An empty list is sorted.
- A list of one element is sorted.
-
A list of two or more elements
(x :: y :: ys)is sorted iff x < y and listy :: ysis sorted.
let rec is_sorted xs =
match xs with
[] -> true
| [_] -> true
| x :: y :: ys ->
if x < y then (is_sorted (y :: ys))
else false
If we forget the case of a single element list, the OCaml compiler will warn us that pattern matching is not exhaustive.
→ A note on lists and tail recursion
The length function was very easy to make tail recursive because it doesn't build a new list in its accumulator.
If we need to build another list, we need to take special care of element order. Since lists can only be built
by prepending a new head to existing tail, accumulating processed list element with :: will reverse the list.
Consider this naive attempt to make map tail recursive:
let rec map f xs acc =
match xs with
[] -> acc
| y :: ys -> map f ys ((f y) :: acc)
let xs = map (fun x -> x * x) [1; 2; 3] []
The xs list is now [9; 4; 1]. A correct implementation must reverse the accumulator before returning it:
let map f xs =
let rec map_aux f xs acc =
match xs with
[] -> acc
| y :: ys -> map_aux f ys ((f y) :: acc)
in List.rev @@ map_aux f xs []
→ Immutability and structural sharing
For primitive values we've worked with before this chapter, immutability doesn't mean much. When closures are not involved, shadowing a variable is not much different from variable assignment since the original value will eventually get garbage collected and lost forever.
Data structures like linked lists is where the benefits of immutability really come into play. Suppose you have multiple functions in your program that are working with the same linked list.
At the machine level, a linked list is a pair of a head value and a pointer to the tail. In a language like C, where you can take any of the pairs that comprise a list and change the head value or the tail pointer, you would be forced to make a complete copy of the entire list if any other functions are also working with it, else you may lose the original list forever.
If values are immutable, the data can be safely shared between multiple functions. When you create a new list by prepending a new head to existing tail, the tail still points to the original tail.
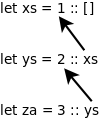
→ Exercises
Using functions from the List module, write a function calculates the sum of squares of all elements in a list.
Rewrite the is_sorted function so that is can use any function for comparing elements rather than just <.
Write a function that reverses a list.
Reimplement the fold_left function in both usual and tail recursive ways.
Write a function that removes all even-numbered elements from a list, e.g. ["foo"; "bar"; "baz"; "quux"; "xyzzy"]
should become ["foo"; "baz", "xyzzy"].